Методики

Выделение штормовых нагонов

Для выделения штормовых нагонов используются ежечасные наблюденные значения уровня моря за штормовые периоды. Штормовые периоды определяются по синоптическим картам. Для того, чтобы уточнить, наблюдался ли в исследуемом пункте нагон или нет, определяются разности между средними суточными уровнями моря за выбранный период и средним месячным уровнем за данный месяц. За штормовой нагон берется лишь тот случай, когда указанная разность превысит 20 см. После этого выбираются сутки с максимальной величиной разности и 2-3 суток до и после максимума (всего для выделения нагона используются как правило 5-7 суток ежечасных наблюдений).

Штормовые нагоны определяются путем вычитания из суммарных ежечасных значений уровня моря предвычисленного прилива. Гармонические постоянные (полуамплитуды и фазы) приливов, по которым предвычисляется прилив, рассчитывались по методу наименьших квадратов (МНК). Наилучшее исключение прилива (суточного и полусуточного) было достигнуто при числе приливных гармоник, равных 21. Метод наименьших квадратов, благодаря своей простоте, гибкости и сравнительно высокой точности, получил широкое распространение при анализе приливов (Zetler B.D., Lennon G.W., 1967; Godin G., 1970; Куликов Е.А., Рабинович А.Б., Харви Р.Р.,1977; Макаева О.С., 1977).

В отличие от классических методов Дарвина и Дудсона, которые для расчета гармонических постоянных требуют использования не менее месячной серии ежечасных значений уровня моря, при использовании МНК для получения такого же количества гармонических постоянных достаточно полумесячной серии. Метод заключается в следующем. В соответствии с теорией гармонического анализа, исходная формула для расчета приливов имеет вид:

где F - редукционный множитель i-той волны; H - средняя полуамплитуда приливного уровня; G - угол положения (фаза) волны; w - угловая скорость волны; t - время; (n0 +u) - начальный астрономический аргумент волны. L - число гармонических постоянных. Для использования МНК формулу (1) удобно представить в виде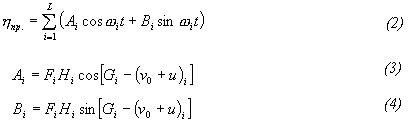

Метод наименьших квадратов заключается в отыскании таких значений коэффициентов Ai и Bi, которые минимизировали бы выражение

где xj - наблюденный уровень в j- тые моменты времени, hj - определяется по формуле (2), N- число отсчетов. Таким образом, задача сводится к решению системы линейных уравнений порядка 2L+1, где L - число рассчитываемых гармоник:

Вычислив таким образом гармонические постоянные L- числа волн, предвычисление прилива осуществляется согласно формуле (1).

Расчет экстремальных суммарных высот уровня редкой повторяемости

Метод основан на статистическом анализе годовых максимумов уровня моря. При этом эмпирическая кривая распределения максимальных уровней, построенная по имеющемуся ряду годовых максимумов, аппроксимируется теоретической функцией распределения, при помощи которой можно экстраполировать эмпирическую функцию в область редких повторяемостей. В качестве такой функции для расчета экстремальных суммарных отклонений уровня использовался двойной показательный закон (Герман В.Х.,1971;Blakman D.L.and Graff J.,1978):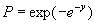

где P -функция распределения; y - приведенная переменная. Согласно статистической теории экстремальных значений, предельные распределения экстремумов могут быть трех типов (первое, второе и третье), отличающиеся видом связи межу приведенной переменной "Y" и статистической переменной "X". Как показывает практика, для пунктов морского побережья эмпирическая функция распределения максимумов уровня имеет вид прямой и соответствует первому предельному распределению. Исходя из этого распределения максимум заданной вероятности определяется по формуле

Оценка параметров первого предельного распределения производится по формуле

где sx - среднее квадратическое отклонение статистической переменной "X" (наблюденного ряда максимумов); X - среднее ряда максимумов; YN - среднее ряда приведенных переменных "Y", соответствующих наблюденному ряду максимумов; sN - среднеквадратическое отклонение ряда приведенных переменных; Приведенные переменные для каждого из наблюденных максимумов вычисляются по формуле

где m - порядковый номер максимума в ряду, расположенном в порядке убывания; Pm - эмпирическая вероятность появления каждого из наблюденных максимумов, рассчитываемая при помощи выражения:

в котором N - число наблюденных максимумов.

Численное гидродинамическое моделирование

Для расчета и прогноза штормовых нагонов в отдельных пунктах побережья Японского моря использованы уравнения мелкой воды (Вольцингер Н.А., Пясковский Р.В.,1968,1977). Двумерная система проинтегрированных по глубине уравнений движения и неразрывности имеет следующий вид: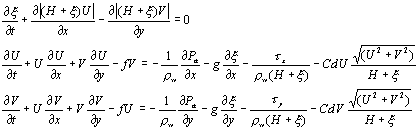

где U, V - осредненные по вертикали составляющие скорости течения по осям "x" и "y"; t - время; x- возвышение поверхности моря над средним уровнем; f =2wSinj -параметр Кориолиса (w - угловая скорость вращения Земли, j - широта места); Pa - приземное атмосферное давление; H - глубина места; rw - плотность морской воды; g -ускорение свободного падения; Cdu, Cdv - коэффициенты трения. Решение этой системы уравнений требует постановки начальных и граничных условий. На твердой границе, расположенной на берегу, нормальные компоненты скорости равны нулю. На жидкой границе возвышение уровня принимается равным нулю, если не учитывается эффект атмосферного давления. В том случае, когда необходимо учесть влияние на уровень вариаций атмосферного давления, условие на жидкой границе принимает вид

где P - среднее атмосферное давление над исследуемым районом; P - атмосферное давление на жидкой границе. Начальные условия принимались нулевыми: x = 0, U = 0, V = 0 при t = 0. Для решения уравнений применялась явно-неявная схема с конечно-разностной сеткой типа "С" (Tong Yongmin, Sun Wenxin, Feng Shizuo,1990; Sun Wenxin, 1992). При этом каждый шаг по времени разбивается на 2 полушага. На первом полушаге решается уравнение по явной схеме определяются значения компоненты скорости V в момент времени n + 1/2.

Затем, используя полученные значения V, по неявной схеме решается уравнение для определения U -компоненты течения. В конечном итоге из уравнения неразрывности по известным значениям U и V значения рассчитываются возвышения уровня в конкретной точке сеточной области. При использовании конечно-разностной сетки типа "С" значения компонент скорости течения вычисляются в узлах сетки, а значения возвышения уровня - в центре квадратов сеточной области. Однако для решения уравнения неразрывности необходимо знать значения U и V в центре квадратов сеточной области, для чего выполняется их осреднение по четырем точкам в каждом квадрате. На втором полушаге этот процесс повторяется. Все пространственные производные рассчитываются со вторым порядком точности. Численная схема не требуют жесткой зависимости между временным и пространственным шагами и позволяет их выбирать оптимальными.