|
В настоящей работе для исследования пространственно-временной
структуры гидрологических параметров и выделения водных масс
Японского моря использованы результаты проведенной поквадратной
обработки всех имеющихся исходных исторических данных глубоководных
океанографических наблюдений. Пространственный масштаб обобщения
информации равнялся 1 градусу широты и долготы, а временной
- 1 месяцу.
Вначале проводилась процедура исключения дублей станций, что
является неизбежным следствием обобщения массового материала
наблюдений, взятого из различных источников. Затем отбраковывались
недостоверные значения элементов с применением предельных
пороговых значений и статистических методов. Приведение информации
на стандартные горизонты производилась посредством линейной
интерполяции.
При расчетах средних многолетних величин во всех квадратах
и на всех стандартных горизонтах для исключения возможно оставшихся
дублей и нормирования вклада суточных многосерийных станций
выполнялась следующая операция. Вначале в каждом квадрате
производилось осреднение всех данных выполненных в конкретные
сутки. Затем полученное осредненное значение в дальнейших
расчетах климатических величин принималось с единичным вкладом.
Эта процедура, главным образом, способствовала исключению
доминирующего вклада информации за отдельные годы, что особенно
важно для квадратов и горизонтов наблюдений с немногочисленным
количеством исходных данных.
Деятельный слой моря в настоящей работе идентифицировался
как слой воды, в котором достоверно выделяются сезонные колебания
океанографических параметров. Оценка достоверности сезонных
вариаций температуры и солености воды на различных горизонтах
была проведена двумя методами. В основу первого (визуального)
положен анализ изменчивости средних многолетних профилей вертикального
распределения от месяца к месяцу. Нижней границей деятельного
слоя в этом случае считался горизонт, на котором ежемесячные
профили становились неразличимы друг от друга.
Второй подход основывается на статистических расчетах. Для
его реализации вначале вся имеющаяся океанографическая информация
была разделена по месяцам. Затем для каждого месяца в квадратах
1° х 1° на всех стандартных горизонтах были рассчитаны средние
величины и их стандартные отклонения. Ошибка выборочных средних
месячных значений на всех стандартных горизонтах в каждом
одноградусном квадрате определялась по формуле:
 ,
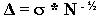где  -
стандартное отклонение, а N - количество наблюдений
[ 34].
Размах сезонных колебаний определялся как разность между максимальными
и минимальными средними месячными значениями характеристик
в квадратах на стандартных горизонтах: 
Если размах сезонных колебаний характеристик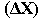 
был больше, чем сумма ошибок для месяцев с экстремальными
значениями  ,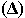
то он считался достоверным.
Верхний квазиоднородный слой (ВКС) идентифицировался как слой
воды с относительно однородным распределением температуры
по вертикали. В этом слое были рассчитаны параметры ВКС (глубина
его нижней границы, средняя температура и соленость слоя).
Для всех параметров были рассчитаны также стандартные отклонения.
Расчеты проведены для квадратов 1° х 1°. Для каждой океанографической
станции было реализовано несколько вариантов идентификации
нижней границы верхнего квазиоднородного слоя:
1. Температура в ВКС отличалась не более чем на 10% от температуры
поверхности моря [62];
2. Для весенних месяцев, когда начинается прогрев поверхностных
вод, в качестве критерия использовались значения температуры
воды не только на поверхности, но и на горизонтах 10, 20 и
30 метров.
На последнем этапе были рассчитаны средние многолетние величины
всех параметров ВКС и их стандартные отклонения.
Анализ результатов двухсуточных наблюдений на станциях основывался
на построенных профилях вертикальных распределений характеристик,
на графиках их временных изменений, а также на статистических
расчетах. Все это позволило оценить меру трансформации профилей
вертикального распределения, выявить временные масштабы колебаний,
определить связность изменений характеристик вод рассматриваемой
толщи от горизонта к горизонту.
В данной работе для обработки данных специальных наблюдений
короткопериодной изменчивости температуры воды также использованы
статистические методы. Обрабатывались ряды, состоящие из временных
колебаний температуры воды и временных вариаций глубины погружения
зонда, на которой измерялась температура воды.
Статистическая обработка проводилась программным комплексом
“Мезозавр” (система анализа временных рядов), который выполняет
большой класс операций, необходимых в статистической обработке
(рассчитывает взаимную корреляционную функцию, дисперсию ряда,
среднее значение, медиану, спектр, периодограмму). В этой
программе есть также модель скользящего осреднения данных.
Последовательность операций при обработке данных специальных
наблюдений заключалась в следующем. В исходных рядах наблюдений
присутствуют нарушения не связанные с временной изменчивостью
температуры воды (это влияния волнения моря и изменения глубины
погружения прибора, связанные с разной скоростью дрейфа судна,
а также, возможно, с пересечением вихревых образований). Поэтому
вначале с помощью уравнения регрессии из рядов температуры
воды исключалось влияние колебаний глубины погружения зонда.
Затем с помощью модели скользящего среднего убиралось влияние
волнения. При сглаживании ширина окна принималась равной 15.
Число 15 было выбрано как наиболее оптимальное исходя из данных
о периодах ветрового волнения и зыби. Анализ метеорологических
данных показал, что периоды ветрового волнения, как правило,
составляют 2-5 сек, а зыби - 4-9 сек. Взаимное влияние рассматриваемых
волн друг на друга может проявляться на периодах, получаемых
из формулы А.И. Дуванина [21]:
Т = N * Тз, где
N=Тз/(Тз-Твв), здесь
Тз - период зыби, а Твв - период ветрового волнения.
Сглаженный ряд температуры воды, после исключения влияния
колебания глубины погружения прибора и волнения, подвергался
дальнейшему последовательному сглаживанию с помощью модели
скользящего среднего. Период осреднения постепенно увеличивался
исходя из графиков предыдущего сглаживания рядов температуры
воды. После каждого сглаживания в ряде остатков определялся
спектр или периодограмма. По графикам и табличным значениям
спектра или периодограммы определялись периоды колебаний температуры
воды, соответствующие ярко выраженным пикам. Из графиков остатков
находился также размах колебаний температуры воды соответствующего
периода.
Оценка доверительных интервалов спектра выполнялась по следующей
схеме. В программе сглаживание спектров производится при помощи
фильтра Парзена. Для этого случая число степеней свободы определяется
по формуле:
 ,
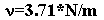где
N - число членов ряда,
m - число задаваемых значений спектра.
Доверительные интервалы для спектральных плотностей определяются
на основе гипотезы о  -
распределении их сглаженных оценок. Зная число n и задавая
уровень значимости b (т.е. процент доверительного интервала),
можно определить множител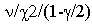и  и
 .
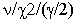Нижняя и верхняя границы ХХ%-го доверительного интервала находятся
умножением оценки S(w) на эти множители. Если основание
спектрального максимума выходит за нижнюю границу доверительного
интервала, то полагается, что максимум значимый.
Для анализа водных масс использован метод TS-кривых, который
был введен Б. Гелланд-Гансеном [85]. Для Японского моря характерно
большое разнообразие форм TS-кривых. Этот факт, а также незначительные
пространственные градиенты температуры и солености в подповерхностных
и глубинных водах, как следует из [37, 47, 48, 54, 72, 97,
108, 121, 122, 124], затрудняют использование этого метода
в качестве основного для анализа климатических данных.
Поэтому в настоящей работе был также использован статистический
T,S-анализ, который предложен Монтгомери [103] Этот метод
получил довольно широкое распространение при исследовании
структуры вод различных частей Мирового океана [1-3, 19, 20,
45, 76, 128]. Детальное описание данного метода представлено
в монографии О.И.Мамаева [41].
Суть метода заключается в следующем. T,S-плоскость разбивается
прямоугольной сеткой на клетки, в каждую из которых заносится
какое-либо значение термохалинного соотношения реальных вод.
Это может быть часть объема вод (термохалинные индексы которых
лежат в элементарных диапазонах), повторяемость наблюдений
за температурой и соленостью, часть общей площади бассейна
с температурой и соленостью, попадающей в отдельные клетки,
и т. д. Оконтуривая на T,S-диаграммах локальные области высокой
повторяемости (“кластеры”) мы получаем, например, индексы
водных масс.
В настоящей работе рассчитывалось частотное распределение
характеристик температуры и солености для отдельных горизонтов
по следующей схеме. В качестве исходных материалов использованы
ежемесячные климатические данные темпе-рату-ры и солености,
полученные путем осреднения в пределах одноградусных квадратов.
Затем эти данные были интерполированы в узлы более мелкой
сетки (0.1° по широте и долготе). Это было сделано для того,
чтобы обеспечить более плавное распределение данных в поле
статистической диаграммы. Таким образом, для построения диаграмм
(например, на поверхности моря) было использовано около 10
000 пар значений температуры и солености.
При расчете конкретных TS-диаграмм выбор интервалов температуры
и солености определялся пространственными пределами величин,
а также возможностью однозначного выделения границ водных
масс и их термохалинных характеристик. Путем численных экспериментов
для поверхностного слоя был выбран интервал 0.5°С и 0.1 промилле.
Для горизонтов ниже 50 м интервалы температуры и солености
уменьшались. Так, например, на горизонте 150 метров они составляли
соответственно 0.25°С и 0.02 промилле, на 300 метров - 0.1°С
и 0.01 промилле, а с 800 метров - 0.005°С и 0.002 промилле.
Результаты на TS-диаграмме представлены в процентах от общего
числа данных.
Предварительный анализ распределения исходных океанографических
данных во времени и в пространстве показал, что в настоящее
время (несмотря на значительное количество имеющейся информации)
на акватории Японского моря нет даже сравнительно небольших
по размерам областей, в которых имелся бы непрерывный пакет
информации за последние 40 - 50 лет. Более того, значительная
нестационарность термических процессов, обусловленная наличием
сезонного тренда, делает невозможным формальное объединение
данных в одну выборку. В этой связи возникает проблема формирования
квазиоднородных выборок, отражающих определенные типы развития
термических процессов, объем которых был бы практически достаточен
для решения поставленных задач.
Поэтому исследуя вопрос о межгодовой изменчивости термического
состояния вод Японского моря естественно полагалось, что формирующиеся
в результате комплекса термодинамических факторов аномалии
температуры воды должны прослеживаться в течение конкретного
года достаточно длительный срок и охватывать значительные
площади. Таким образом, для исключения сезонного тренда термических
процессов при анализе многолетней изменчивости, данные о температуре
воды предварительно центрировались, то есть представлялись
в виде отклонений от средних многолетних месячных значений
на горизонте 100 м в каждой точке.
Для анализа пространственно-временной структуры гидрометеорологических
полей в последние десятилетия хорошо себя зарекомендовал метод
разложения полей по эмпирическим ортогональным функциям (ЭОФ)
[6, 7, 53]. Одним из его достоинств является возможность разделить
пространственные и временные составляющие изменчивости. Выделение
отдельных составляющих изменчивости и оценка их весов базируется
на учете статистической структуры самих исходных полей, то
есть анализируются взаимосвязи всех точек поля (разложение
проводится по корреляционной или ковариационной матрице).
Однако имеющиеся пропуски данных гидрометеорологической информации,
делают невозможным эффективную реализацию данного метода.
Подобная ситуация особенно выражена при анализе гидрологических
условий на дальневосточных морях, где систематизированное
накопление данных начато относительно недавно.
В связи с эти возникает проблема: как провести разложение
исходных полей по ЭОФ с одновременным восстановлением пропущенных
значений (без или с минимальным искажением реальной статистической
структуры анализируемых полей). Наиболее рациональным подходом,
по-видимому, является использование методов оптимизации, основанных
на итерационных схемах расчета [17, 53, 60]. Достоинствами
этих схем являются: универсальность относительно широкого
класса задач, простота вычислительного процесса, малое количество
промежуточных данных, устойчивость к ошибкам округления и
т.д. Оптимизационная задача поиска пропущенных значений (Аs.)
сводится к следующему. В процессе вычислений необходимо подобрать
такие пропущенные значения, которые бы минимизировали оценку
определенного функционала (критерия согласия), отражающего
степень точности разложения исходных полей по ЭОФ и последующего
их восстановления. В качестве начального приближения пропущенных
данных можно использовать средние многолетние значения. Затем
реализуется итерационный процесс подбора таких пропущенных
значений, которые бы оптимальным образом отражали статистическую
структуру анализируемого поля представленную эмпирическими
ортогональными функциями. При этом в качестве минимизируемого
функционала рационально использовать наиболее показательные
критерии согласия [5, 9, 53, 71]:
(1)
где Yk , Fk - фактические и восстановленные
значения соответственно, N - объем выборки.
Выбор конкретного критерия согласия из представленного списка
(1) определяется целевой направленностью решаемой задачи.
Формально решение сводится к определению в многомерном пространстве
минимума критерия согласия (1). В основу метода минимизации
положен алгоритм покоординатного спуска с периодическим вращением
осей координат [9, 17, 60, 71]. При этом начальное приближение
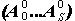 вычисляется
в виде среднего многолетнего или задается в потоке входных
данных.
Итерационный процесс продолжается до выполнения условия окончания
минимизации: достижения заданного значения критерия согласия
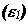 или
предельно допустимой величины  ,
где  -
изменения в минимизируемых функциях (Фе) от итерации
к итерации.
Использование различных критериев согласия диктуется желанием
получить наиболее оптимальную аппроксимацию, зависящую от
целей анализа. Например, при анализе экстремальных ситуаций
лучших результатов, по-видимому, следует ожидать при использовании
минимаксного критерия. Использование же критерия наименьших
квадратов приводит к притягиванию пропущенных значений к средним.
Кроме того, традиционно используемый метод наименьших квадратов
(МНК) [7, 9, 53] предъявляет к исходной информации весьма
жесткие требования, что для реальных данных зачастую не выполняется.
Поэтому получаемые в этих условиях оценки оказываются недостаточно
эффективными. Помимо этого, оценки МНК очень неустойчивы в
области малых выборок, а при восстановлении пропущенных значений
в полях гидрометеорологических характеристик объем информации,
как правило, ограничен. Определенные перспективы просматриваются
также при совместном анализе результатов, полученных при реализации
различных критериев согласия [53, 60].
В настоящей работе для восстановления пропущенных значений
и оптимального отображения статистической структуры полей
применялся изложенный выше алгоритм реализованный в виде пакета
программ.
В качестве критерия согласия использовался критерий суммы
модулей (Ф3), как некоторый альтернативный вариант между критерием
наименьших квадратов (Ф1) дающим аппроксимацию близкую к среднемноголетним
распределениям и критерием минимакса Ф2, притягивающим восстанавливаемые
значения к имеющимся экстремальным [5, 53, 60, 71]. Начальное
приближение задавалось в виде средних многолетних значений
температуры воды в каждой точке.
Затем исходные поля температуры воды подвергались процедуре
разложения по ЭОФ. Процедура разложения по ЭОФ достаточно
традиционна и подробно описана в публикациях [6, 7, 9]. После
этого проводилось восстановление исходных полей, но лишь по
первым наиболее крупномасштабным собственным функциям, в сумме
несущих заданное количество информации об изменчивости исходных
полей. Данная процедура позволяет несколько сжать информацию
и иллиминировать незначительные, близкие к случайным флуктуации
параметров. Исходные и восстановленные значения в одноименных
точках поля сравнивались по критерию согласия. На следующем
шаге начальные приближения пропущенных значений изменялись
и процедура счета повторялась до тех пор пока не были найдены
такие значения, которые приводили к минимуму задаваемого функционала.
Рассчитанные по этим значениям ЭОФ представляли оптимальную,
в смысле поставленной задачи, статистическую оценку пространственно-временной
структуры анализируемых полей.
В дальнейшем, с целью минимизации возможных ошибок в исходных
и восстановленных данных, а также подавления мелкомасштабных
флуктуаций параметров выбранные для анализа поля подвергались
процедуре сглаживания. В качестве сглаживающего оператора
использовалась формула пространственного осреднения с весами
обратно пропорциональными расстоянию до узла сглаживания (i).
 ,
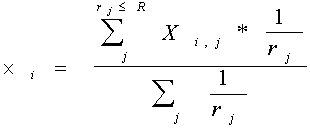где Xi,j - узлы сетки попавшие в окружность с радиусом
R, где r=R. При этом в самом узле сглаживания
радиус принимался равным единице (При i = j, r =
1).
Выбор предельного радиуса сглаживания является весьма важной
и неоднозначной задачей, которая диктуется поставленными целями
исследования. Однако, предложенный алгоритм сглаживания применим
для целого класса задач, он упрощает процедуру выбора максимального
радиуса сглаживания (R), так как веса оператора обратно пропорциональны
расстоянию и при увеличение расстояния от узла сглаживания
веса составляющих быстро уменьшаются. В настоящей задаче максимальный
радиус сглаживания принимался равным 150 миль. Таким образом
в процедуре сглаживания для каждого узла сетки (2°*2°) участвовали
только данные соседних с ней узлов.
После процедуры сглаживания исходное поле представлялось в
виде разложения по эмпирическим ортогональным функциям.
Разумеется, проведенный анализ не исчерпывает всего многообразия
проблем, возникающих при анализе изменчивости гидрометеорологических
полей и разработке моделей прогнозирования гидрометеорологических
процессов. Так, даже в рамках поставленного эксперимента возникает
вопрос оценки эффективности восстановления пропущенных значений
и представления статистической структуры поля в зависимости
от выбранного критерия согласия. Ясно, что с переходом от
критерия наименьших квадратов к другим критериям следует расширять
методологическую базу оценок восстановления, так как традиционные
оценки не будут уже отражать всего многообразия предъявляемых
к решаемой задаче требований. Следовательно, необходимо вводить
оценки, отражающие принципы, заложенные в самих критериях
согласия.
|
