Долгосрочный прогноз

Реализация вероятностной модели для прогноза ледовых характеристик на Японском море

Метод априорных условных вероятностей

Задача построения алгоритма сводится к нахождению условных вероятностей Р (Фj / Dli) j ... 1, k ; i ... 1, n ; l ... 1, L. Здесь Фj - вероятность появления j-й градации ледовитости, Dli - дискретная область изменения предиктора, где l - номер конкретного предиктора i - номер градации, где k, n - количество градаций предиктанта и предиктора соответственно, L - общее число предикторов. Весьма существенным препятствием на пути использования этого метода является то, что число состояний вектора предиктора оценивается как:

где nl - число градаций l-го предиктора очень быстро растет с ростом n и L. В результате некоторые состояния вектора предиктора могут быть не обеспечены данными. Поэтому на данном этапе рассматривался ряд конкурирующих моделей вероятностного прогноза, реализующих нахождение условных вероятностей только от одного предиктора. В этом случае матрица условных вероятностей рассчитывается так:

Или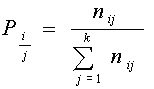

где nij - число случаев, когда при появлении градации предиктора i наблюдается фаза предиктанта j. Соответственно прогноз будет иметь вид: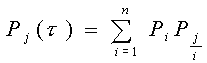

где Рj(t) - вероятность появления j-й градации ледовитости, Рi - вероятность появления i-й градации предиктора, t - заблаговременность прогноза. При этом механизм заблаговременности можно учитывать: а) непосредственно, закладывая сдвиг по времени t в матрицу условных вероятностей Pj/i = Pj/i. Соответственно уравнение преобразуется к виду: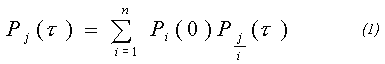

где Р (0) - вектор начальных условий, Рi = 1 для наблюдавшейся градации предиктора, Рi = 0 - для всех остальных; б) рассчитывая предварительно прогностические значения Рi = Pi (t), что приводит к следующему выражению:

Однако последний вариант более трудоемок, так как дополнительно требует реализации некоторого прогностического алгоритма для оценки вероятности Рj(t). В связи с этим основное внимание уделялось расчетам по формуле (1). Рассчитывались матрицы условных вероятностей появления определенной фазы ледовитости по каждому из предикторов (формы циркуляции А.А. Гирса, О.К. Ильинского, температуры поверхностного слоя воды) с заблаговременностью от одного до шести месяцев. Так как гидрологические процессы обладают большей инерционностью по сравнению с атмосферными, при использовании в качестве предиктора осредненного значения температуры воды расчеты проводились при сдвигах t до девяти месяцев. Используя полученные матрицы, был дан вероятностный прогноз по всему спектру заблаговременностей на вторую декаду января для 10 лет, выбранных с помощью генератора случайных чисел, и рассчитаны оценки Брайера.

где Pj и Pj0 - фактическое и прогностическое значения фазы предиктанта; соответственно N - количество прогнозов. (Рj = 1 для осуществившейся фазы и Рj = 0 для всех остальных). Оценка Брайера определяет меру ошибочности прогнозов и равна единице для идеального прогноза. В целом полученные оценки показали приемлемость и перспективность данного подхода.

Сравнительный анализ оценок прогноза позволил провести ранжирование используемого на данном этапе архива предикторов (формы циркуляции А.А. Гирса, О.К. Ильинского, температура воды) по степени информативности в задаче вероятностного прогнозирования ледовитости Японского моря. Максимальная информативность при апробации моделей прогноза отмечалась для индексов О.К. Ильинского. Оптимальная заблаговременность составила один месяц. Информативность индексов А. А. Гирса и показателей термического режима вод несколько ниже и соизмеримы между собой. Для показателей термического режима оптимальная заблаговременность оказалась около 9 месяцев. Это, вероятно, связано с существенной инерционностью этого показателя и выражает влияние весеннего теплонакопления на последующий ледовый режим. Следовательно, можно считать, что при заблаговременности прогноза не более трех месяцев превалирующую роль в формировании ледовых условий играют атмосферные процессы. При более долговременных связях заметный вклад в перераспределение гидрометеорологических условий начинает вносить тепловая инерция морей.

Модель цепей Маркова

Использование для вероятностного прогноза ледовитости марковских моделей и, в частности, цепей Маркова - один из возможных путей решения поставленной задачи. Как известно, временные корреляционные функции рядов декадных значений ледовитости асимптотически стремятся к нулю, что, в свою очередь, является характерной особенностью марковской модели. Этот факт послужил основной предпосылкой для апробации модели простой цепи Маркова применительно к задаче прогноза перераспределения ледовитости на Японском море. Для последовательности градаций ледовитости за 1960-1993 гг. была расcчитана матрица переходных на следующую декаду вероятностей: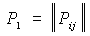

где i - предшествующее состояние, j - последующее состояние системы, которая послужила исходным материалом для декадных прогнозов ледовитости. Предполагая однородность простой цепи Маркова, прогноз осуществлялся как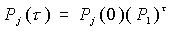

Здесь Рj(t) - ожидаемые вероятности появления различных градаций ледовитости, Pj(0) - начальное состояние ледовитости, t - заблаговременность прогноза.

При увеличении заблаговременности матрица (P1)t стремится к своему предельному значению, характеризующемуся минимумом прогностической информации (максимумом энтропии). Подобный вывод следует и из анализа оценок Брайера, рассчитанных по проверочной последовательности (десяти наугад выбранным годам) (см. таблицу в п. «Метод априорных условных вероятностей»), где видно, что оценки при превышении заблаговременности один месяц ухудшаются. Таким образом, использование данной модели для прогноза перераспределения декадных ледовитостей Японского моря с заблаговременностью больше одного месяца представляется нецелесообразным. При меньших заблаговременностях модель показала вполне удовлетворительные результаты. Следовательно, учитывая простоту и наглядность, модель после соответствующей проверки можно рекомендовать для практического использования.

Байесовский прогноз

Достоинством этого подхода является то, что он позволяет объединить различные источники информации для формулирования вероятностного прогноза в условиях не столь жестких, как в ряде других методов. Кроме того, Байесовский метод дает возможность учитывать неформализованную информацию посредством включения субъективных вероятностей, отражающих сведения, полученные на основе индивидуального опыта. Идея Байесовского метода заключается в том, что, объединяя априорную функцию плотности распределения вектора параметров (или априорные вероятности событий) с информацией выборки, получают апостериорную функцию плотности распределения (или апостериорные вероятности событий). Задача заключается в построении вычислительного алгоритма (3) , с помощью которого в любой конкретной ситуации известному вектору-предиктору оптимальным образом приводилась бы в соответствие ледовитость Японского моря. Для конкретной разработки задача ставилась более узкая: требовалось провести только оптимизацию заданного алгоритма. Прогностический оператор строился на основе формулы Байеса:

где Фj - одно из возможных значений фаз предиктанта, Х0 - значение текущего вектора предикторов, i - номер предиктора, Ф (Хi /Фj ) - условные повторяемости каждой градации каждого предиктора при каждой фазе ледовитости. Для удобства построения и использования условных функций распределения все переменные преобразовывались из непрерывных в дискретные. При дискретизации значения переменной Хit заменялись номерами градаций, в которые они попадали. Границы градаций вычислялись так, чтобы градации были равными: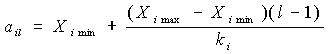

где Хmax и Хmin - максимальные и минимальные значения переменной, i - номер переменной, ki - число градаций, l - номер градации, аil - граничные значения переменной. Преобразованный таким образом архив представлялся в виде { Di, Фj } , где Di - осуществившаяся в ситуации t градация предиктора , а Фj - соответствующая данной ситуации фаза предиктанта (ледовитости). На данном архиве оцениваются статистические параметры модели: 1. Условные повторяемости каждой градации каждого предиктора при каждой фазе предиктанта.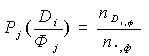

2. Их климатическая повторяемость.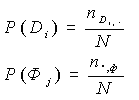

3. Коэффициенты Чупрова, служащие для оценки сопряженности предиктора X с конкретным предиктантом.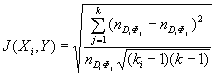

где nDiФj - число совмещений градации Di и фазы Фj; nDi,. - общее число осуществления Di; n.,ф - общее число осуществлений j-й фазы Ф ; nDiФj - число совмещений при независимости X и Y. Количество фаз предикторов и предиктантов можно задавать произвольно, но, учитывая ограниченность рядов наблюдений в расчетах, желательно, чтобы число градаций не превышало пяти. В данных конкретных расчетах число градаций задавалось равным трем. Отбор оптимального состава предикторов осуществлялся в следующей последовательности. На первом этапе из архива выбирался наиболее информативный для данного предиктанта предиктор, то есть тот, которому соответствовало максимальное значение коэффициента Чупрова (maxJ(x,y)). Затем на произвольно выбранном ряду данных (использовались данные за 10 выбранных случайным образом лет) определялась успешность прогноза. Последующий состав предикторов отбирался на основе критерия Брайера (2). Строилась итерационная схема: отбирался предиктор, дающий вместе с уже отобранным на первом этапе по J(xi,y) максимум оценки (2), потом пара, тройка, и т.д. предикторов до тех пор пока не достигалось "насыщающего" значения оценки, т.е. улучшение качества прогнозов практически прекращается, несмотря на учет новых переменных. Расчеты показали, что условия "насыщения" происходят уже при учете 6-8 предикторов. Можно, разумеется, отбор предикторов организовать только при помощи оценки Брайера (2), то есть первый предиктор выбирать не по критерию Чупрова (J), а также по максимуму (B). Однако первый вариант несколько предпочтительней, так как дает возможность получения ряда альтернативных комбинаций предикторов, сравнение результатов использования которых позволяет повысить устойчивость работы модели.

Оценка успешности Байесовского метода вероятностного прогноза

С целью испытания предложенной прoгностической схемы проводился прогноз декадной ледовитости Японского моря с заблаговременностью до 6 месяцев. Для сокращения общего объема вычислений прогноз рассчитывался только на вторую декаду каждого месяца. Предполагалось, что оценки прогнозов на остальные декады месяца не слишком отличаются от полученных и их непосредственный учет не имеет принципиального значения при общем суждении о возможности использования данного метода. Авторские испытания метода при прогнозах по данным 10 случайным образом выбранных лет с заблаговременностью до 6-ти месяцев показали достаточно высокие результаты.

При этом оценки Брайера в основном изменялись в пределах 0.75-0.95, а процент оправдываемости нередко достигал 100% ,что свидетельствует об успешности реализации данной схемы для прогноза ледовитости. При этом оправдавшимся считался прогноз при котором предсказание правильной градации предиктанта осуществлялось с вероятностью более 50%. Анализ повторяемостей отбираемых в процессе прогноза предикторов свидетельствует о достаточно устойчивом механизме влияния процессов происходящих в атмосфере и океане на формирование ледовых условий. Так, повторяемость учета температуры воды, в определяемых списках наиболее информативных предикторов при различных прогнозах, близка к 100%. Одновременно, выбор этого показателя в качестве первого - доминирующего фактора осуществлялся с повторяемостью не превышающей 8%. Как правило, в качестве первого наиболее информативного предиктора выступал тот или иной показатель крупномасштабной атмосферной циркуляции: чаще всего характеристики алеутской депрессии, охотского антициклона или индексы зональной циркуляции. Относительная же информативность термического состояния поверхностного слоя воды несколько выше при прогнозах ледовитости в начальный период ледового сезона (декабрь-январь). Ошибочные прогнозы обычно связаны с резкой сменой характера гидрометеорологических процессов уже внутри интервала заблаговременности, что приводит к неучтенному прогнозом радикальному перераспределению ледовых условий. В вероятностном плане это выражается в изменении типа зимы (по характеру ледовых условий). Например, неудачные прогнозы были получены для зимы 1967-68 гг., когда развитие ледовых условий по типу ледовитых зим (декабрь-январь) сменилось на малоледовитый тип (февраль-март). Другой пример это 1980-81 гг., когда малоледовитый тип зимы в начальный период (декабрь-январь) сменился ледовитым в завершающий (март-май). Базируясь на приведенных оценках и учитывая, что существующие долгосрочные прогнозы в категорической форме еще далеки от совершенства, а вероятностные прогнозы практически отсутствуют, предложенную схему для долгосрочного вероятностного прогноза ледовитости, а также и ряда других ледовых характеристик, можно рекомендовать для практического использования. В дополнение можно сказать, что она в силу своей универсальности может найти применение при исследовании вероятностной структуры природных объектов и разработке вероятностных моделей прогноза различных гидрометеорологических параметров.

Метод прогноза ледовитости, основанный на алгоритмах МГУА (метод группового учета аргументов)

Попытка решить задачу долгосрочного прогноза с помощью традиционных линейных моделей множественной регрессии не привела к положительным результатам. Хотя отдельные коэффициенты корреляции при исследовании асинхронных связей ледовитости с комплексом показателей атмосферной циркуляции и достигали достаточно высоких значений, но в целом для долгосрочного прогноза по спектру заблаговременностей от 1 месяца до года регрессионные связи оказались недостаточно тесными. Как правило, множественный коэффициент корреляции не превышал величину 0,64. Тем не менее, для ориентировочных консультационных прогнозов модели множественной линейной регрессии с набором предикторов из приведенного выше архива, выбираемых по признаку максимума коэффициента корреляции, в силу их простоты и наглядности могут быть рекомендованы. Невозможность хорошей аппроксимации зависимости ледовитости от комплекса параметров в пространстве простых линейных связей привело к необходимости поиска более сложных статистических отношений между предиктантами и предикторами. Для реализации подобных задач высокие результаты можно получить, используя методы группового учета аргументов (МГУА). В результате численных экспериментов из возможных алгоритмов МГУА была синтезирована модель прогноза, являющаяся некоторой суперпозицией алгоритмов последовательного выделения оптимальных трендов и частных линейных описаний. В частности, предлагается схема прогноза.

Блок - схема долгосрочного прогноза ледовитости

Архив информации, содержащий данные о предиктантах и предикторах, с помощью генератора случайных чисел разбивается по заданному соотношению (в нашем конкретном случае как 2:1) на две выборки - обучающую и проверочную. На обучающей последовательности методом наименьших квадратов строятся два ряда частных описаний предиктантов последовательно от каждого из заданного числа предикторов: - ряд степенных полиномов:

где ai - весовые коэффициенты данного полинома, рассчитываемые методом наименьших квадратов; - ряд по тригонометрическим функциям: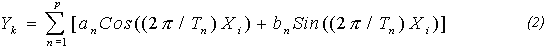

где an и bn - коэффициенты Фурье, вычисляемые методом наименьших квадратов. Индекс суммирования p показывает количество членов полинома в уравнениях (1) или количество выделяемых гармоник в уравнении (2). При этом максимальное количество членов уравнения (1, 2) ограничивается объемом обучающей выборки N:

Это значение (max P) и определяет максимально возможную сложность рассчитываемого тренда* (уравнений 1-2). В качестве тренда оптимальной сложности для каждого ряда описаний отбирались зависимости, минимизирующие на проверочной последовательности среднюю квадратическую ошибку прогноза. При переборе трендов в список кандидатов в переменные первым номером всегда включалось время. Это связано с возрастанием роли функции времени при увеличении заблаговременности прогноза. После этого рассчитывались функции от всех возможных сочетаний, выделенных на предшествующих этапах трендов (здесь и далее под трендом понимается функция от любого аргумента, а не только времени):

В целях сокращения вычислительных процедур функция трендов представлялась только в виде некоторого степенного полинома. Например, для трех трендов она имела вид:

Количество членов полинома (5) также ограничивалось условием (3). Затем последовательно отбрасывалось по одному члену, имеющему минимальный коэффициент корреляции с предиктантом и выбиралось уравнение, минимизирующее на проверочной последовательности среднюю квадратическую ошибку прогноза. Данная процедура выполняется параллельно для всех рассчитанных на предшествующих этапах сочетаний (функций трендов) степенных и тригонометрических трендов. После этого из совокупности полученных в результате всех операций функций отбирались две оптимальных (одна для полиномиальных зависимостей между предиктантом и предиктором и одна для тригонометрических представлений), минимизирующих s. Однако в силу недостаточного объема исходной информации количество одновременно анализируемых трендов (зависимостей вида 1-2) для последующего построения функции (5) ограничивалось пятью (рассматривались все сочетания, включающие от двух до пяти уравнений вида 1-2). При необходимости учета максимально возможного количества предикторов, включались те, которые не вошли в отобранное сочетание (4-5), дополнительно использовались частные описания типа: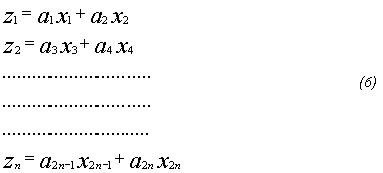

Здесь xi - предикторы, не вошедшие в отобранное сочетание вида (4-5), 2n - общее количество предикторов, а - коэффициенты уравнений, полученные методом наименьших квадратов, z - невязка прогноза по уравнению для функций трендов.

Для дальнейшего сжатия информации рассчитывалось множественное уравнение регрессии относительно невязки прогноза с использованием функции трендов (оптимального сочетания отобранных на первых этапах предикторов), где в качестве предикторов выступали частные описания вида (3):

Количество слагаемых в сумме (8) также регламентируется длиной обучающей последовательности. Соответственно, при необходимости учета большего количества факторов генерируется ряд альтернативных уравнений регрессии, то есть реализуется направленный перебор вариантов использования различных наборов предикторов. Отбор оптимального уравнения регрессии происходит по материалам тестирования на проверочной выборке. Результирующий прогноз получается как суперпозиция по функции трендов и множественного уравнения регрессии от оставшихся предикторов:

При оперативном использовании схемы после осуществления всех операций по формированию прогностической модели (9) следует запрос данных о предикторах (прогностические данные) и осуществляется прогноз. При этом выдается два параллельных результата, соответствующих видам частных описаний трендов (степенной полином или ряд по тригонометрическим функциям), дальнейший анализ, сравнение и выбор одного из которых выполняется непосредственно экспертом, заинтересованным в прогнозе. Изложенная схема реализована в виде пакета программ и широко используется в практике. Оценки качества метода, рассчитанные согласно требованиям, предъявляемым к долгосрочным прогнозам по проверочной последовательности на примере прогноза ледовитости для второй декады марта с заблаговременностью не ниже шести месяцев, приведены в таблице 4.

Как следует из таблицы, наиболее удачные прогнозы получены при использовании в качестве доминирующих параметров аномалий температуры (DТ) в Охотском антициклоне. Возможно, характер аномальности Охотского антициклона и является некоторым долгосрочным индикатором мартовских ледовых процессов на Охотском и Японском морях. Приемлемые результаты получены и с использованием в качестве доминирующих факторов членов разложения в ряд Фурье аномалий температуры летней дальневосточной депрессии, северо-американского минимума или степенных полиномов для аномалий по северному полюсу. Достаточно хорошие оценки получены и для показателей термического режима воды. Испытания метода на проверочной последовательности показали среднюю оправдываемость прогнозов с заблаговременностью до 6-ти месяцев за весь ледовый период (декабрь-май) по акваториям Японского моря около 78%. Минимум оправдываемости - порядка 65% - падал на начальный период ледового сезона. Как правило, тренды по тригонометрическим функциям несут меньшую ошибку по сравнению с полиномиальными представлениями (для DТ арктического антициклона разложение в ряд Фурье не проводилось). Это, по-видимому, связано с большей устойчивостью тригонометрических функций, рассчитанных на ограниченной выборке, по сравнению со степенными полиномами. Из представленного списка предикторов отмечается некоторое повышение информативности для показателей, учитывающих процессы за периоды апрель-май и август-сентябрь.